CCSS Math Activities
Satellite
This isn't rocket science, you know. A performance task has learners use right triangle trigonometry to calculate distances from stations on Earth to a satellite. It also requires finding the distance between two stations along the...
101 Questions
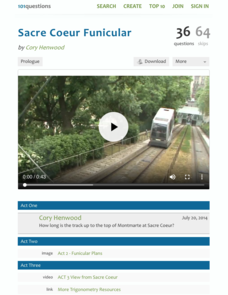
Sacre Coeur Funicular
Rise to the challenge of trigonometry. Watching a video of an ascending funicular at the Sacre Coeur in Paris sets the stage for a challenging task. Young mathematicians use a given diagram, along with the concepts of slope and...
101 Questions
Laying Sod
Lay out a firm understanding of trigonometry. Scholars watch a video recording of a worker laying sod on a lawn. Given the dimensions of each piece of sod and the lawn, they determine how many pieces of sod are necessary. Trigonometry...
101 Questions
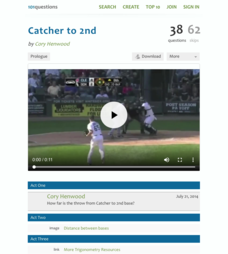
Catcher to 2nd
Who's on second? Young mathematicians use a diagram of a baseball field to find the distance a catcher must throw to reach second base. A brief video of such a play during a baseball game sets the stage for the assignment.
101 Questions
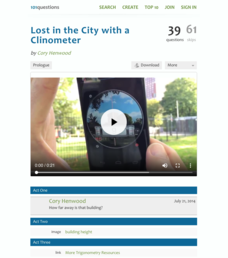
Lost in the City with a Clinometer
Come look at trigonometry from a different angle. To begin a simple activity, scholars view a video of someone using a clinometer to find the angle of elevation to the top of a building. They then use a diagram that shows the building's...
101 Questions
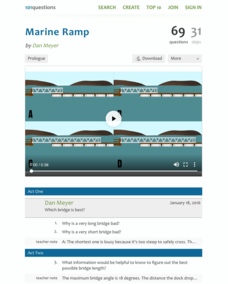
Marine Ramp
Boat ramps move with waves and changes in water level. Scholars decide on the proper length for a ramp so the angle connecting both sides is appropriate. They visualize the situation and use a simulation to view the results with their...
National Council of Teachers of Mathematics
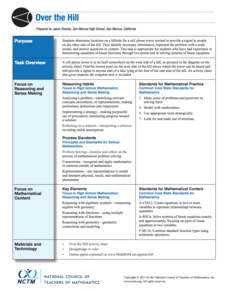
Over the Hill
Can you hear me from there? Pupils determine the place to build a cell tower on a hill. The class uses constraints and creates a scale drawing on a coordinate system to calculate the exact location of the base of the cell tower.
National Council of Teachers of Mathematics
Tidal Waves
Periodically ship the class a trigonometric application. Pupils model the level of water in a port. Using their models, learners determine the times that a ship can safely navigate into and out of the port, along with determining other...
NOAA
Through Robot Eyes
How do robots assist ocean explorers in collecting data and images? The final installment in a five-part series has science scholars examine underwater images collected by robots and identify the organisms shown. Groups then calculate...
CK-12 Foundation
Possible Triangles with Side-Side-Angle
It's not often that math allows for multiple answers. Young mathematicians identify possible numbers of triangles when given two sides and a non-included angle. An interactive helps with this investigation.
CK-12 Foundation
Angle-Angle-Side Triangles: Garden Gate
Good fences make good gardens. Individuals use an interactive to see how angles and sides relate in a triangular-shaped garden fence. They apply the Law of Sines to find the length of the garden gate (third side of triangle) given two...
CK-12 Foundation
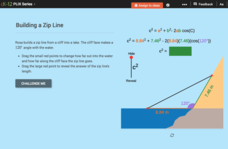
Law of Cosines: Building a Zip Line
Zip this resource into your lesson plans. Here is an interactive that shows how angles and lengths change based on conditions for a zip line. Scholars use the Law of Cosines to solve problems in this context.
CK-12 Foundation
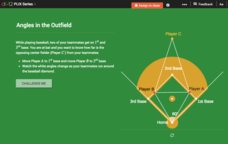
Law of Cosines: Angles in the Outfield
Take me out to the trig class. Individuals use an interactive to see how angles on a baseball field change as the position of two runners change. A set of challenge questions has them apply the Law of Cosines to solve problems.
CK-12 Foundation
Ambiguous Case: Furniture Store Problems
Remove any ambiguity about using a helpful resource. Individuals use an interactive to find the number of triangles that fit given conditions. They find that some conditions can result in more than one triangle in the ambiguous case.
CK-12 Foundation
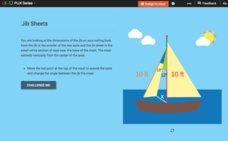
Determination of Unknown Triangle Measures Given Area: Jib Sheets
Solving triangles is a breeze. Young boat enthusiasts solve problems involving triangles in the context of sails on a boat. They must apply different strategies, including the Law of Cosines and area formulas.
CK-12 Foundation
Law of Cosines: Baseball Diamond
Catch a great resource! Individuals use an interactive that allows them to move players on a baseball field. They calculate distances between players using the Law of Cosines.
CK-12 Foundation
Law of Cosines: Get on Base
Baseball is all about math. Young baseball and mathematics enthusiasts determine the distance between players on a baseball field using the Law of Cosines. An interactive helps them find relevant distances and angles to use in their...
CK-12 Foundation
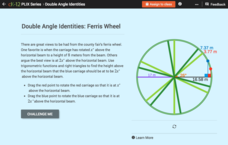
Double Angle Identities: Ferris Wheel
Use a Ferris wheel to soar to new heights of understanding on double angle identities. Here is an interactive that applies an example of a Ferris wheel to show how doubling the angle does not double the value of a trigonometric ratio....
CK-12 Foundation
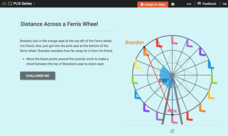
Length of a Chord: Distance Across a Ferris Wheel
An interactive presents two friends on a ferris wheel with the task of finding the distance between the them. Pupils create the chord between the two friends and calculate its lengths using trigonometric ratios.
CK-12 Foundation
Right Triangles, Bearings, and Other Applications: Sailing Race
Help your class get their bearings when it comes to right triangles. Pupils determine distances traveled or components given the bearing of a sailboat using an interactive. The scholars develop a sense of finding the bearings of a given...
CK-12 Foundation
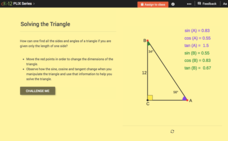
Pythagorean Theorem for Solving Right Triangles: Solving the Triangle
Observe the change in the trigonometric ratios as angles vary. An interactive provides the values of trigonometric ratios for both acute angles in a right triangle. Pupils create a right triangle to match given criteria and find the...
CK-12 Foundation
Secant, Cosecant, and Cotangent Functions: Hold the Ladder!
Determine the length of a falling ladder. Pupils use an interactive to find the angle a ladder makes with the floor after it falls to answer questions. The scholars use the triangle formed in the interactive to determine values of...
CK-12 Foundation
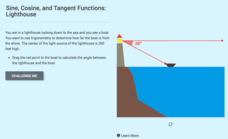
Sine, Cosine, and Tangent Functions: Lighthouse
How far is that boat from the lighthouse? Scholars create diagrams to represent a scenario given the angle of depreciation from a lighthouse to a boat. Learners apply the basic trigonometric functions to find various distances stemming...
CK-12 Foundation
Angles of Elevation and Depression: Fly-By Calibration
Determine the distance between two trees from afar. Pupils use an interactive resource to create two right triangles using trees and a plane. They determine the horizontal legs of each triangle to find the distance between the two trees.