Curated OER
The Pythagorean Puzzle
An engaging hands-on activity is presented. Learners of all ages are addressed in thie unique plan. K-5 learners identify, name, and define a rectangle, square, triangle, and the concept of area. Older learners prove the Pythagorean...
Radford University
The Pythagorean Theorem in Crime Scene Investigation
It's a Pythagorean who-dun-it. Pupils apply the Pythagorean Theorem in several different real-world scenarios involving right triangles. By solving each task, they find the thief who was responsible for a museum heist.
EngageNY
Proof of the Pythagorean Theorem
What does similarity have to do with the Pythagorean Theorem? The activity steps through the proof of the Pythagorean Theorem by using similar triangles. Next, the teacher leads a discussion of the proof and follows it by an animated...
Shodor Education Foundation
Pythagorean Explorer
Make sure the measurement is right. The interactive provides right triangles with a missing side measurement. Pupils use the given sides and the Pythagorean Theorem to calculate the length of the missing side. After entering the length,...
Virginia Department of Education
The Pythagorean Relationship
Add up areas of squares to discover the pythagorean relationship. Small groups create right triangles with squares along each side. They calculate the areas of each square and notice the relationship. Groups construct other types of...
Shodor Education Foundation
Squaring the Triangle
Teach budding mathematicians how to square a triangle with an interactive that shows a graphical proof of the Pythagorean Theorem. Pupils alter the lengths of the legs using sliders. Using the inputted lengths, the applet displays the...
Mathematics Vision Project
Similarity and Right Triangle Trigonometry
Starting with similar triangles and dilation factors, this unit quickly and thoroughly progresses into the world of right triangle features and trigonometric relationships. Presented in easy-to-attack modules with copious application...
Radford University
Right Triangle Applications: Lessons 1 and 2
Use right triangles for more than just mathematical problems. The first two lessons of a unit ask pupils determine distances between cities by using the Pythagorean Theorem and a map. To cement understanding, learners use trigonometric...
Radford University
Getting Around Millbrook
When is the distance formula not accurate? Referencing a map of the school, pairs determine the walking distance between two locations. Creating coordinates for each location, pupils determine the distance between the two points and...
Illustrative Mathematics
Eratosthenes and the Circumference of the Earth
The class gets to practice being a mathematician in ancient Greece, performing geometric application problems in the way of Eratosthenes. After following the steps of the great mathematicians, they then compare the (surprisingly...
Virginia Department of Education
Distance and Midpoint Formulas
Small groups work through two guided activities to derive the distance and midpoint formulas for the coordinate plane. The activities begin with concrete examples and move to abstract.
Curated OER
Access Ramp
Just about every public building that your students are familiar with has an access ramp which complies with ADA requirements. As it turns out, designing such a ramp is an excellent activity to incorporate slope, the Pythagorean Theorem,...
DiscoverE
Build a Cable-Stayed Bridge
Large or small, bridges are architectural wonders! Construct a large-scale cable-stayed bridge during a whole class project. Scholars work in groups to erect the towers, build the roadway, and secure the cables of their very own bridges....
Illustrative Mathematics
The Lighthouse Problem
Long considered the symbol of safe harbor and steadfast waiting, the lighthouse gets a mathematical treatment. The straightforward question of distance to the horizon is carefully presented, followed by a look into the...
Mathematics Vision Project
Module 6: Congruence, Construction, and Proof
Trace the links between a variety of math concepts in this far-reaching unit. Ideas that seem very different on the outset (like the distance formula and rigid transformations) come together in very natural and logical ways. This...
Mathalicious
Been Caught Stealing
You're safe, when calculating the odds of stealing second base! Learners compare the rate of a runner to the distance the ball travels, in a lesson that explores right triangles and measurement. Full of discussion questions and fun...
Illustrative Mathematics
Extensions, Bisections and Dissections in a Rectangle
Gaining practice in translating a verbal description into a diagram and then an equation is the real point of this similar triangles exercise. Once the diagram is drawn, multiple methods are provided to reach the conclusion. An effective...
Math Stars
Math Stars: a Problem-Solving Newsletter Grade 8
You've just hit the jackpot of integrating math problems and riddles with this jumbo-sized resource! Written as a newsletter, scroll through 35 pages of puzzles and quality problems to engage and encourage your learners to inquire...
Mathematics Vision Project
Module 7: Connecting Algebra and Geometry
The coordinate plane links key geometry and algebra concepts in this approachable but rigorous unit. The class starts by developing the distance formula from the Pythagorean Theorem, then moves to applications of slope. Activities...
Curated OER
Is This a Rectangle?
How do you show that something is a rectangle? This activity starts with four coordinate points and asks young geometers to explain whether they create a rectangle. Knowledge from both geometry and algebra come into play here, as well...
Curated OER
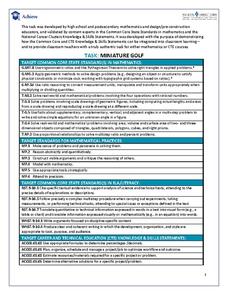
Task: Miniature Golf
"Fore!" All right, no one really yells this out in miniature golf, but this well-defined activity will have your charges using lots of numbers in their unique design of a miniature golf hole. Included in the activity criteria is the...
Radford University
Football Tackle Problem
Tackle a task on the gridiron. Scholars use geometric concepts to determine the distance on a coordinate plane that certain football players need to move for a play. They then design their own plays and create presentations where they...
Radford University
Running Laps During Soccer Practice
Which option involves running less? Given a situation in which players can either run around the school soccer field 20 times or run back and forth along the diagonal 20 times, learners decide which option would be better. They consider...
University of Colorado
Designing an Open Spectrograph
Take the class over the rainbow. Pairs or small groups follow directions to create a spectrograph. The pupils measure the angles formed by the different colors of the spectrum along with calculating the lengths formed by the spectrum and...