FuseSchool
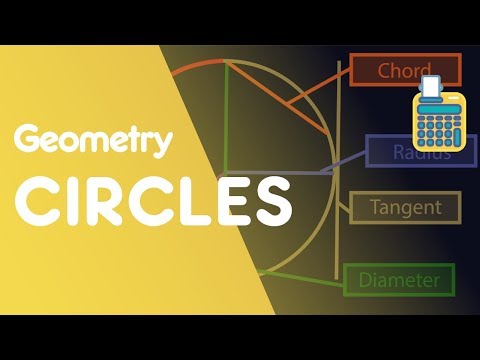
Circle Terminology - Radius Diameter Sector Segment Chord Arc Tangent
DESCRIPTION: There are some key words we need to know for circles: radius, circumference, diameter, sector, segment, tangent, chord and arc. In this video we discover what they all mean. The radius is the distance from the centre of a...
Brian McLogan
Find the central angle given the arc length and radius
👉 Learn how to solve problems with arc lengths. You will learn how to find the arc length of a sector, the angle of a sector, or the radius of a circle. An arc of a circle is the curve between a pair of points on the circumference of the...
Curated Video
Find Measures of Inscribed Angles Using Central Angles
In this video, the teacher explains the relationship between the measure of an inscribed angle and its intercepted arc. They use the central angle theorem to prove and apply this relationship. By understanding this theorem, students can...
Curated Video
Circle Terminology - Radius Diameter Sector Segment Chord Arc Tangent | Geometry | Math | FuseSchool
DESCRIPTION: There are some key words we need to know for circles: radius, circumference, diameter, sector, segment, tangent, chord and arc. In this video we discover what they all mean. The radius is the distance from the centre of a...
Brian McLogan
What is the relationship for two inscribed angles with the same endpoints
Learn how to solve problems with arcs of a circle. An arc is a curve made by two points on the circumference of a circle. The measure of an arc corresponds to the central angle made by the two radii from the center of the circle to the...
Flipped Math
Intercepted Arcs
Intercept the class's learning on circles. Pupils learn the relationship between intercepted arcs and inscribed angles. The scholars use that information to find the relationship of angles in an inscribed quadrilateral and an angle...
Krista King Math
Degree Measure of an Arc
Circular patterns and movement are commonplace in our world. Young mathematicians begin their study of circles with instruction on finding the degree measure of both major and minor arcs. Examples focus on the arc in relation to the...
Krista King Math
Inscribed Angles of Circles
Relationships in circles build from the many connections made throughout the geometry course. The instructor in the video explains these connections as she builds the concept of inscribed angles. Using examples, the narrator highlights...
CK-12 Foundation
Inscribed Angles in Circles: Lesson
Circle the angles and intercept the arcs. The video introduces three theorems relating to inscribed angles in circles. Using drawings, the segment of a playlist on geometry illustrates the measure of angle along with theorems about two...
Corbett Maths
Angles in the Same Segment – Proof
If angles intercept the same arc, the angles must be the same size. The quick video talks through the proof of showing the reason two inscribed angles that intersect the same arc have the same measurement. Pupils then create their own...
Khan Academy
Khan Academy: Geometry: Ca Geometry: Secants and Translations
Demonstrates solutions to problems #76-80 of California Geometry released state test questions. Problems address tangents to circles, secants to circles, intercepted arcs, translations on the coordinate plane, and rotations on the...
Sophia Learning
Sophia: Secant Lines: Lesson 3
This lesson introduces the concept of secant lines. It is 3 of 5 in the series titled "Secant Lines."
Sophia Learning
Sophia: Secant Lines: Lesson 2
This lesson introduces the concept of secant lines. It is 2 of 5 in the series titled "Secant Lines."
Sophia Learning
Sophia: Secant Lines: Lesson 1
This lesson introduces the concept of secant lines. It is 1 of 5 in the series titled "Secant Lines."
Khan Academy
Khan Academy: Geometry: Inscribed and Central Angles
Proof that the measure of an inscribed angle is half the measure of a central angle when the angles intercept the same arc. [14:16]
Khan Academy
Khan Academy: Inscribed Shapes: Find Inscribed Angle
Using either the inscribed angle theorem or the fact that two inscribed angles that intercept the same arc must be congruent.