Hi, what do you want to do?
Curated OER
Who am I? Find A Polynomial From Its Roots
High schoolers generate the equation of a polynomial given its roots and the end behavior of the function. They need to apply theorems concerning the multiplicity of roots, conjugates of irrational or imaginary roots to find a...
Curated OER
T Points from Directions
Here is a lesson that starts with having geometers translate points using compass directions into an accurate picture of the problem. Then they must use their knowledge of the Pythagorean theorem or similar triangles to solve. This makes...
Mathematics Vision Project
Module 3: Polynomial Functions
An informative module highlights eight polynomial concepts. Learners work with polynomial functions, expressions, and equations through graphing, simplifying, and solving.
Curated OER
Arithmetic Complex Numbers
Young scholars convert quadratic functions from standard form to vertex form. In this algebra instructional activity, students solve polynomials using synthetic and long division. They derive and apply the remainder theorem and factor...
Mathematics Vision Project
Module 3: Numbers and Operations
Bring some concrete reasoning to the skills of multiplying and combining terms. Using various strategies, the six activities in the module provide practice for the skills of adding, subtracting, multiplying, and diving polynomials. The...
Curated OER
Worksheet 17
In this math learning exercise, students practice graphing functions and define the domain. Then they use Lagrange's Theorem to estimate the error involved in using the two Taylor polynomials.
Curated OER
Exercise Set 3.3: Dividing Polynomials
In this dividing polynomials worksheet, high schoolers divide 42 polynomials. Students factor polynomials using synthetic division and long division.
EngageNY
The Special Role of Zero in Factoring
Use everything you know about quadratic equations to solve polynomial equations! Learners apply the Zero Product Property to factor and solve polynomial equations. They make a direct connection to methods they have used with quadratic...
Curated OER
Polynomial Divisions
Students factor polynomials and use long division t solve problems. In this algebra lesson, students find the zeros of polynomials by synthetic and long division. They perform operation using complex numbers.
Curated OER
Exploring the Landscape
Students determine the monotonicity and concavity properties of a function, then apply the First Derivative Test and draw conclusions about the first and second derivatives from these properties.
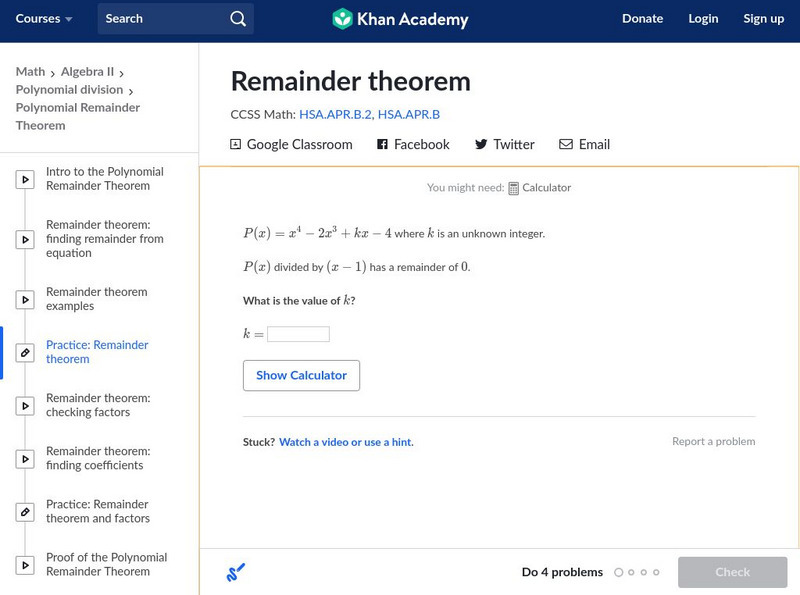
Khan Academy
Khan Academy: Algebra Ii: Remainder Theorem
Use the PRT (Polynomial Remainder Theorem) to determine the factors of polynomials and their remainders when divided by linear expressions. Students receive immediate feedback and have the opportunity to try questions repeatedly, watch a...
Interactive Mathematics
Interactive Mathematics: The Remainder and the Factor Theorem
This tutorial contains a lesson about the remainder and factor theorems along with practice problems.
Math Planet
Math Planet: Algebra 2: Polynomial Functions: Remainder and Factor Theorems
Provides examples and a video lesson that illustrate the remainder and factor theorems. [1:34]
McGraw Hill
Glencoe Mathematics: Quiz on the Remainder and Factor Theorems
The online assessment demonstrates knowledge of advanced mathematical concepts in Algebra II. The questions test students on the remainder and factor theorems.
Texas A&M University
Wtamu Virtual Math Lab: College Algebra: Synthetic Division
This tutorial will show you how to use synthetic division and how to use both the remainder and factor theorems in conjunction with synthetic division. Offers several examples with solutions and explanations as well as practice problems...
Windstream
Ojk's Precalculus Study Page: Remainder and Factor Theorems
An introduction to two important uses of synthetic substitution, the remainder theorem and the factor theorem. Includes examples and sample problems with solutions.
Illustrative Mathematics
Illustrative Mathematics: A Apr the Missing Coefficient
The purpose of this task is to emphasize the use of the Remainder Theorem as a method for determining structure in polynomials in equations, and in this particular instance, as a replacement for division of polynomials. Aligns with...
Illustrative Mathematics
Illustrative Mathematics: A apr.b.3 and a apr.b.2: Graphing From Factors Iii
The task has students use the remainder theorem to deduce a linear factor of a cubic polynomial, and then to completely factor the polynomial. Aligns with A-APR.B.3 and A-APR.B.2.
Khan Academy
Khan Academy: Zeros in the Quotient (No Remainders)
Practice solving division problems with 0s in the solution, or quotient. Students receive immediate feedback and have the opportunity to try questions repeatedly, watch a video or receive hints.
Lawrence Hall of Science
The Math Page: Topics in Pre Calculus: Synthetic Division by X A
Here is a site that clearly and thoroughly explains how to divide a polynomial by a binomial using synthetic division. There are example problems solved, problems for the student to attempt, and answers to the student problems. Point...
Illustrative Mathematics
Illustrative Mathematics: A Apr Zeroes and Factorization of a General Polynomial
In this task, students investigate the properties of a polynomial of degree d > 0. The task relates to the Fundamental Theorem of Algebra. Aligns with A-APR.B.2.
National Council of Teachers of Mathematics
The Math Forum: Ask Dr. Math: Partial Fractions
Math Forum offers a description of remainder and factor theorem and gives and example of their uses.
Illustrative Mathematics
Illustrative Mathematics: A Apr Zeroes, Factorization of Quadratic Polynomial Ii
This task is intended to help students see more clearly the link between factorization of polynomials and zeroes of polynomial functions. The argument here generalizes to show that a polynomial of degree d can have at most d roots....
Illustrative Mathematics
Illustrative Mathematics: A Apr Zeroes and Factorization of Quadratic Polynomial
This is the first of a series of problems building to an understanding of an important property of polynomial functions, that a polynomial of degree d can have at most d roots. Aligns with A-APR.B.2.