CK-12 Foundation
Volume by Cross Section: Volume of the Cone
Discover another way to find the volume of a cone. Pupils explore how the area of a cross section changes as it moves through a cone. The interactive uses that knowledge to develop the integral to use to find the volume of the cone....
CK-12 Foundation
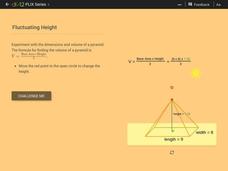
Volume of Pyramids: Fluctuating Height
The height of a pyramid may change, but the usefulness of the interactive will not. Learners drag the apex of a pyramid to change its height. They then answer a set of challenge questions designed to investigate how changing the...
CK-12 Foundation
Volume by Disks: The Vase Case
Finding the volume is an integral characteristic of a vase. Using the idea that summing the areas of cross-sectional disks will calculate the volume of a rotational solid, pupils find the volume of a vase. Scholars determine the interval...
Discovery Education
Sonar & Echolocation
A well-designed, comprehensive, and attractive slide show supports direct instruction on how sonar and echolocation work. Contained within the slides are links to interactive websites and instructions for using apps on a mobile device to...
CK-12 Foundation
Method of Cylindrical Shells
Approximate the volume of a solid of revolution. Using a method similar to approximating the area under a curve, pupils investigate the volume of a solid of revolution. The learners use a given definite integral to find the volume of...
CK-12 Foundation
Algebra Expressions with Exponents: Fish Tank Cube
There's nothing fishy about this resource. A slider interactive lets users adjust the side length of a fish tank cube. It aids in seeing changes in the volume and how to express the volume using an algebraic expression.
CK-12 Foundation
Linear, Quadratic, and Cubic Models: The Box Model
Models make math manageable. Individuals investigate a cubic function that models the volume of a cube through the interactive.
CK-12 Foundation
Monomial Factors of Polynomials: Mystery Boxes
Shortcut the work in finding total volumes. Pupils determine a polynomial expression that would represent the combined volume of three boxes. Each box has the same height, and the scholars rewrite the expression by factoring out the...