CK-12 Foundation
Volume by Cross Section: Volume of the Cone
Discover another way to find the volume of a cone. Pupils explore how the area of a cross section changes as it moves through a cone. The interactive uses that knowledge to develop the integral to use to find the volume of the cone....
CK-12 Foundation
Area and Volume of Similar Solids: Similar Solids
Five questions make up an interactive designed to boosts knowledge of area and volume of solid figures. Question types include multiple-choice, true or false, and fill-in-the-blank. A scale model changes measurement to provide a visual...
CK-12 Foundation
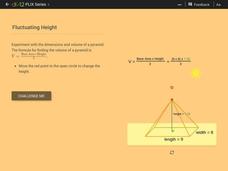
Volume of Pyramids: Fluctuating Height
The height of a pyramid may change, but the usefulness of the interactive will not. Learners drag the apex of a pyramid to change its height. They then answer a set of challenge questions designed to investigate how changing the...
CK-12 Foundation
Volume by Disks: The Vase Case
Finding the volume is an integral characteristic of a vase. Using the idea that summing the areas of cross-sectional disks will calculate the volume of a rotational solid, pupils find the volume of a vase. Scholars determine the interval...
CK-12 Foundation
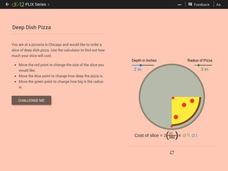
Linear Equations: Deep Dish Pizza
Explore the volume of solids with a real-life connection. Learners calculate the volume of a deep-dish slice of pizza to determine its price. They model the slice as a part of a cylinder and create a formula for calculating the cost.
CK-12 Foundation
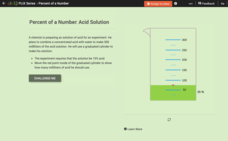
Percent of a Number: Acid Solution
Mathematicians answer five questions about percents, ratios, and proportions with help from an interactive graduated cylinder. Question types include multiple-choice, fill-in-the-blank, and discussion.
CK-12 Foundation
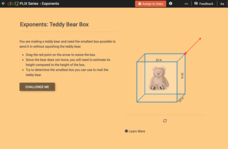
Whole Number Exponents: Teddy Bear Box
Five questions—multiple-choice, fill in the blank, and discussion—make up an interactive that challenges scholars to mail a teddy bear using the smallest box possible without squishing it. A box with movable sides allows mathematicians...
CK-12 Foundation
Absolute Extrema and Optimization: Building the Biggest Box
Optimally, you want the largest box. Given a square piece of box material, pupils determine the size of congruent squares to cut out of the corners to create a box with the greatest volume. Learners determine the equation of the volume...
CK-12 Foundation
Method of Cylindrical Shells
Approximate the volume of a solid of revolution. Using a method similar to approximating the area under a curve, pupils investigate the volume of a solid of revolution. The learners use a given definite integral to find the volume of...
CK-12 Foundation
Algebra Expressions with Exponents: Fish Tank Cube
There's nothing fishy about this resource. A slider interactive lets users adjust the side length of a fish tank cube. It aids in seeing changes in the volume and how to express the volume using an algebraic expression.
CK-12 Foundation
Linear, Quadratic, and Cubic Models: The Box Model
Models make math manageable. Individuals investigate a cubic function that models the volume of a cube through the interactive.
CK-12 Foundation
Sum and Difference of Cubes: Stacking Blocks
Investigate polynomial factoring patterns by finding a connection to volume. As learners build a three-dimensional solid from smaller solids, they convert the visual model to a mathematical expression. Their models represent the sum of...
CK-12 Foundation
Monomial Factors of Polynomials: Mystery Boxes
Shortcut the work in finding total volumes. Pupils determine a polynomial expression that would represent the combined volume of three boxes. Each box has the same height, and the scholars rewrite the expression by factoring out the...
PBS
Pbs Learning Media: Floating and Sinking: Hot Air Balloons
Why do hot air balloons float? This resource from the NOVA Web site offers a series of interactive activities that illustrates the physics of hot air balloons.