Curated OER
The Konigsberg Bridge Problem
In this Konigsberg Bridge problem worksheet, students solve 35 short answer problems. Students construct networks consisting of even and odd vertices. Students make conjectures about the number of odd and even vertices on a vertex-edge...
West Contra Costa Unified School District
Conics Introduction and Parabolas
Where did conic sections get their name? The equation and graph of a parabola are developed from the definition of the conic section. Teacher examples on graphing the equation and writing an equation from the graph round out the plan.
Curated OER
Plane, Graphs and Paths
In this plane learning exercise, students provide that a graph is bipartite, identify the paths, and identify a planar graph. This one-page learning exercise contains five problems.
Curated OER
Practice Exam Part 1: Vocabulary
In this geometry instructional activity, students practice constructing a variety of graphs with various degrees of vertices. Students determine whether 12 graphs have an Euler circuit or path.
Concord Consortium
Painted Stage
Find the area as it slides. Pupils derive an equation to find the painted area of a section of a trapezoidal-shaped stage The section depends upon the sliding distance the edge of the painted section is from a vertex of the trapezoid....
Old Dominion University
Introduction to Calculus
This heady calculus text covers the subjects of differential and integral calculus with rigorous detail, culminating in a chapter of physics and engineering applications. A particular emphasis on classic proof meshes with modern graphs,...
Curated OER
Match Game: Enrichment
In this solid figures activity, students choose a shape from the box that fits the bar graph totals for the faces, edges, and vertices. Students then complete the last bar graph using the one unused shape.
Code.org
Algorithms Detour - Minimum Spanning Tree
This optional lesson plan introduces the class to the idea of a minimum spanning tree. The activity focuses on determining an algorithm that will find the most efficient path in a network to transfer data.
Curated OER
Travel Problems
This worksheet is actually an entire chapter focused on math problems involving, shortest path, minimum connector, traveling salesman, and Chinese postman problems. There are multiple activities, exercises, and examples to get students...
Curated OER
Tracing Worksheet
In this geometry activity, students explore graphing characteristics. Students complete seven short answer and problem solving questions about graphing and whether or not one can be traced.
EngageNY
Perimeter and Area of Polygonal Regions in the Cartesian Plane
How many sides does that polygon have? Building directly from lesson number eight in this series, learners now find the area and perimeter of any polygon on the coordinate plane. They decompose the polygons into triangles and use Green's...
EngageNY
Finding Systems of Inequalities That Describe Triangular and Rectangular Regions
How do you build a polygon from an inequality? An engaging lesson challenges pupils to do just that. Building from the previous lesson in this series, learners write systems of inequalities to model rectangles, triangles, and even...
Curated OER
Math Matching Worksheet
In this math worksheet, students match math vocabulary to definitions and then solve problems using Euler's theorem and Fleury's algorithm. Students complete 24 problems.
Curated OER
Worksheet 34
In this math worksheet, students find the plane perpendicular to the path (t2, t, cos 2πt) at time t = 1/4. Then they determine the location in which the object is moving the fastest.
Wolfram Research
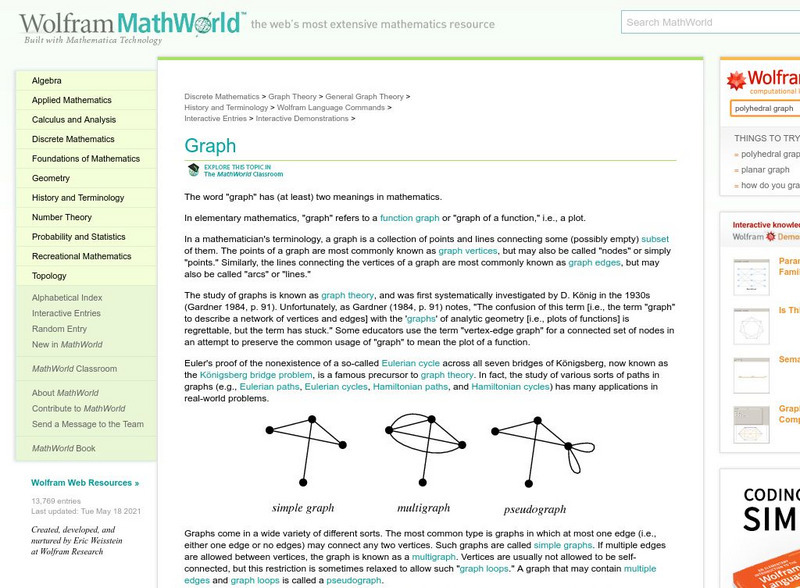
Wolfram Math World: Graphs
MathWorld.com shows many types of discrete math graphs and provides links to related topics.
Other
Geeks for Geeks: Graph and Its Representations
The choice of graph representation is situation-specific. It totally depends on the type of operations to be performed and ease of use. This reference explains the most commonly used representations of a graph: Adjacency Matrix and...
Other
Tutorials Point: Graph Theory Coloring
Graph coloring is nothing but a simple way of labeling graph components such as vertices, edges, and regions under some constraints. This site introduces you to graph coloring and its applications in the real world.
Other
Geeks for Geeks: Graph Coloring|set 1 (Introduction and Applications)
Graph coloring problem is to assign colors to certain elements of a graph subject to certain constraints. This source looks at different applications of graph coloring.
Wolfram Research
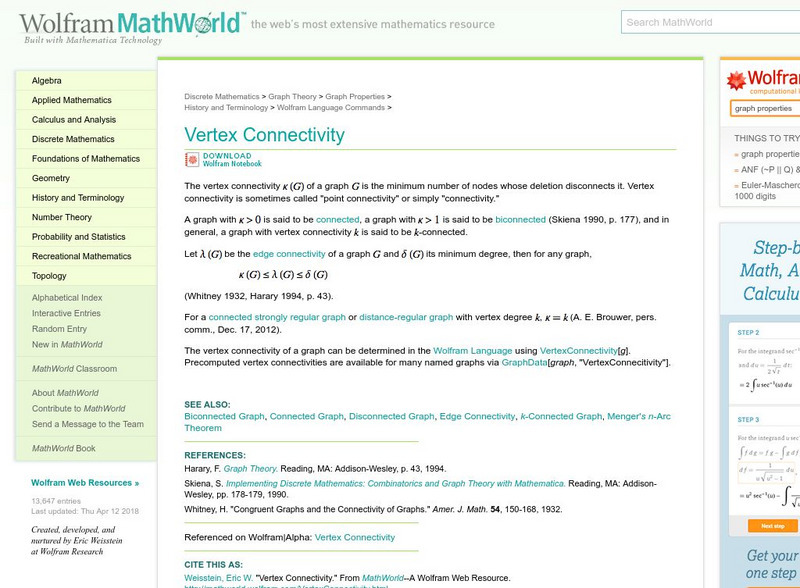
Wolfram Math World: Vertex Connectivity
A description of vertex connectivity, that relates to edge connectivity.
Wolfram Research
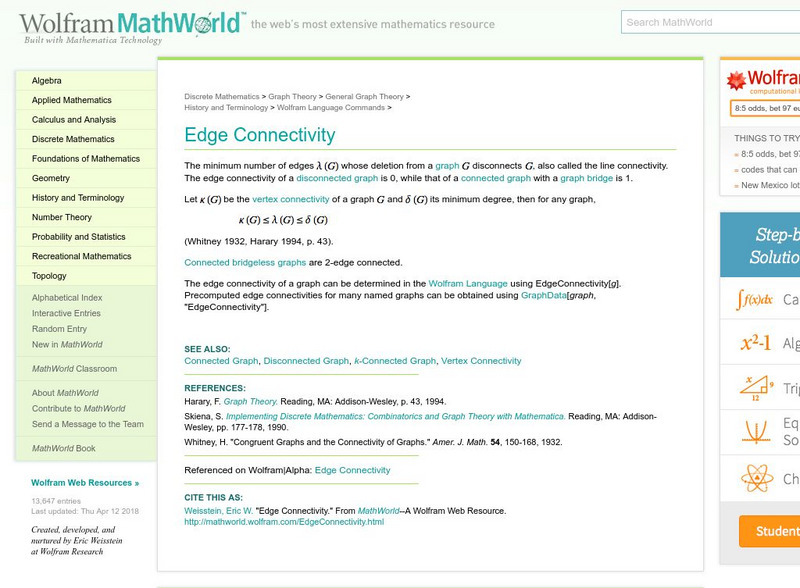
Wolfram Math World: Edge Connectivity
A description of edge connectivity, that relates to vertex connectivity.
Wolfram Research
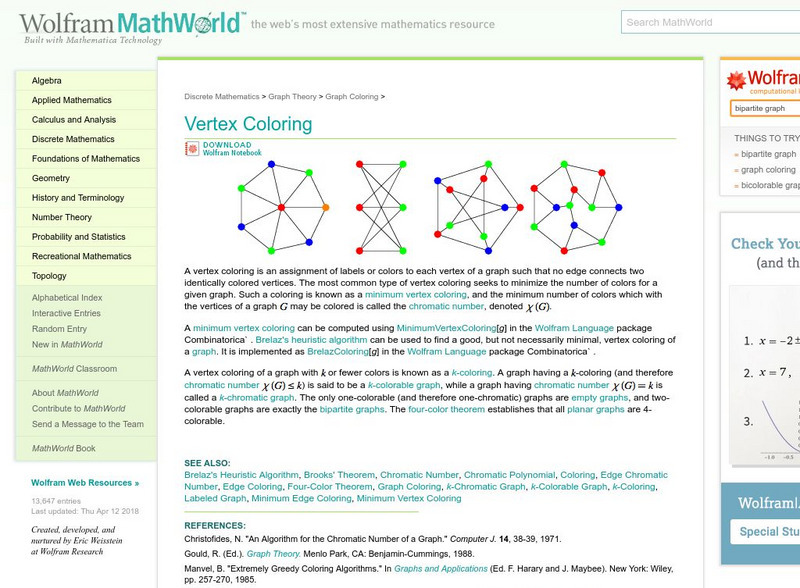
Wolfram Math World: Vertex Coloring
You will find a definition and diagrams dealing with vertex coloring.
Wolfram Research
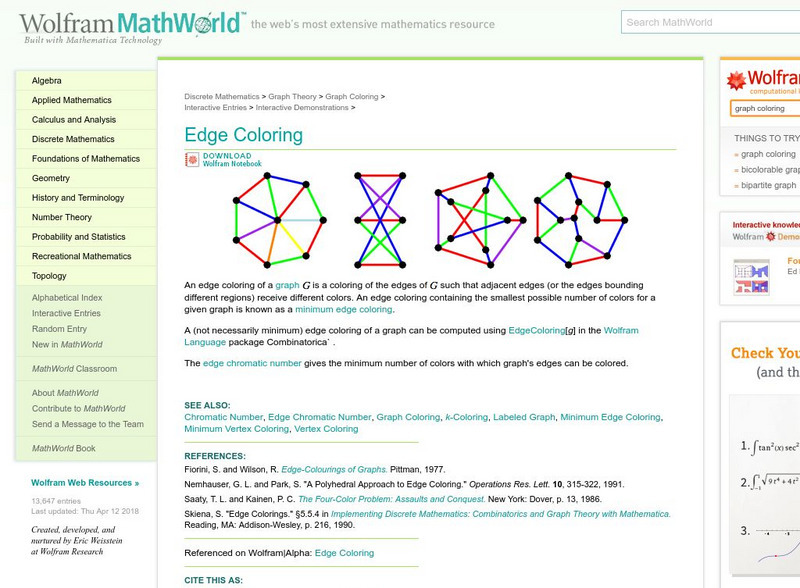
Wolfram Math World: Edge Coloring
This site displays a description and diagrams dealing with edge coloring.
Other popular searches
- Vertex Edge Graph Worksheets
- Vertex Edge Graph Mapping
- Vertex Edge Graph Map
- Vertex Edge Graphs Maps
- Vertex Edge Graphs Mapping
- Vertex Edge Graphs Matrices
- Color Vertex Edge Graphs
- Vertex Edge Graphs Euler
- Hamilton Vertex Edge Graphs
- 3rd Grade Vertex Edge Graphs