Mathematics Vision Project
Transformations and Symmetry
Flip, turn, and slide about the coordinate plane. Pupils define the rigid motions and experiment with them before determining the relationships of the slopes of parallel and perpendicular lines. The sixth unit in a nine-part series...
CK-12 Foundation
Horizontal Translations or Phase Shifts: Cosine
If cosine is shifted, how is its equation affected? Learners manipulate the graph of cosine by moving the y-intercept to different locations on the coordinate plane. Pupils determine the new equation that models the shifts.
CK-12 Foundation
Horizontal Translations or Phase Shifts: Tangent
Patterns can be shifty! Find the pattern when shifting the graph of tangent. Pupils move the graph of tangent to different locations on the coordinate plane. They observe what happens to the function and its vertical asymptotes...
CK-12 Foundation
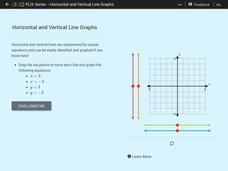
Horizontal and Vertical Line Graphs
See how vertical and horizontal lines have special equations. Scholars drag vertical and horizontal lines onto a coordinate plane to graph given equations. They then answer a set of challenge questions on the topic.
CK-12 Foundation
Linear Inequalities in Two Variables
Take the tediousness out of finding solutions of inequalities by graphing. Individuals use an interactive that allows them to adjust a system of inequalities on a coordinate plane. Using the interactive helps find solutions to systems of...
CK-12 Foundation
Graphs of Linear Functions: Line Designs
Designs from lines are sublime. Scholars create colorful designs by connecting points on an interactive coordinate plane. They answer questions about slope and quadrants based on their designs.
CK-12 Foundation
Standard Form of Linear Equations: Seesaw
Don't hem and haw, learn about equations using a seesaw. An easy-to-use interactive has pupils move a seesaw on a coordinate plane to investigate the standard form of a linear equation. By completing a set of challenge questions, they...
CK-12 Foundation
Forms of Linear Equations: Equation Exploration
Different forms, same line. Young mathematicians investigate the standard form, slope-intercept form, and point-slope form of a linear equation. An interactive has them adjust lines on a coordinate plane to see changes in each form of...
CK-12 Foundation
Comparing Equation of Parallel and Perpendicular Lines: Parallel and Perpendicular Lines
It seems perpendicular lines have slopes which follow a specific rule. Scholars use an interactive to investigate this rule by moving a pair of lines on a coordinate plane. They find that perpendicular lines have slopes that are opposite...
CK-12 Foundation
Distance Between Two Points: Biking the Blocks
Distance estimates would be easy if the world were a grid. Scholars work to determine the distance between two structures using a coordinate plane. As an introduction, the lesson focuses on vertical and horizontal distances.
CK-12 Foundation
Evaluate Limits Using Graphs and Tables: Where Is That Limit?
Limits are made easy through graphs and tables. An easy-to-use interactive lets users change a function on a coordinate plane. They relate graphs and tables to the limit at a specific value.
CK-12 Foundation
Infinite Limit Type: Evaluating Limits of Rational Functions
Rational functions become less mysterious when you know about limits. Individuals use an interactive to move a rational function on a coordinate plane and to investigate function values for certain x-values. They see how the limit...
CK-12 Foundation
Restricted Domain and Range: Translation of a Curve
Moving the graph of a function obviously changes its domain and range. Scholars adjust the location of a graph in an interactive coordinate plane. The interactive automatically updates and displays the domain and range to show how it...
CK-12 Foundation
Vector Projection
Two words summarize the interactive: vector projector. An easy-to-use resource lets users investigate vector projections on the coordinate plane. Given the components of two vectors, they determine the projection of one vector onto the...
CK-12 Foundation
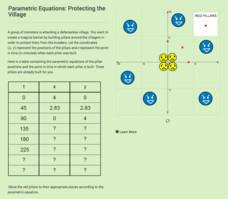
Parametric Equations: Protecting the Village
Determine the location of the pillars in time. Given a table of values for two parametric equations, pupils complete the table to determine the location and time it takes to build the pillars. Learners plot the points representing...
National Council of Teachers of Mathematics
Over the Hill
Can you hear me from there? Pupils determine the place to build a cell tower on a hill. The class uses constraints and creates a scale drawing on a coordinate system to calculate the exact location of the base of the cell tower.
CCSS Math Activities
Social Security Trust Fund
Will Social Security still be around when you retire? Given data on the predicted balance of the social security fund over time, scholars plot the points on a coordinate grid and determine if a quadratic regression fits the data. They...
Mathematics Vision Project
Module 1: Transformations and Symmetry
No need to change anything about the resource. The first of eight modules in the MVP Geometry unit focuses on transformations in the coordinate plane. It connects translations, rotations, and reflections to congruence, symmetry, and...
Radford University
Finding a Location for Your Kitchen Island
Where is the best place to work? Small groups map out a kitchen on a coordinate plane and find the centers of the work triangle to find the best place to install an island. The teams use algebraic methods to locate the center by finding...
Radford University
Football Tackle Problem
Tackle a task on the gridiron. Scholars use geometric concepts to determine the distance on a coordinate plane that certain football players need to move for a play. They then design their own plays and create presentations where they...
Radford University
Discovering Quadratics
Get to know quadratics from a couple of different perspectives. Classmates work in small groups to determine the optimal cooking time for microwave popcorn. Group members pop bags of popcorn for different times and collect data on the...
Radford University
How to Calculate and Analyze the Equation for a Parabolic Path
Working in groups, pupils plot three points on the coordinate plane representing three different parabolic paths. Using a calculator, they determine the quadratic regression equation for their models. Each team then figures out the...
Utah Education Network (UEN)
Geometry
Shape one's understanding of geometry using the resource. The sixth of seven chapters in 6th Grade Math focuses on geometry principles. Future mathematicians learn to find the area of parallelograms, trapezoids, triangles, and other...
Math by Design
Transformations – Reflections
Scholars use interactive resources to figure out how to mathematically draw a reflection of a geometric shape viewed in a mirror. To conclude the activity, class members are asked to deduce the result of multiple reflections across...