Balanced Assessment
Number Game
It's all in the numbers! Create a mathematical model to analyze a number game and develop a winning strategy. Using a given numerical pattern, scholars write an expression to model the scenario. They then interpret the pattern of the...
NOAA
It All Runs Downhill
Examine how pollution makes its way into an ocean with help from a model watershed. Scholars use household items to recreate a mini-watershed, equipped with pollutants, that when mixed with rain drain into a model's body of...
101 Questions
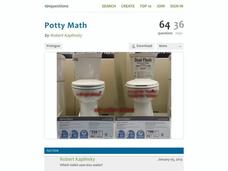
Potty Math
You don't want to flush your money down the drain! Have your classes complete a financial comparison between two different types of toilets. They use linear modeling to determine the most cost-effective model.
Concord Consortium
Bill the Ball Bearing Man
Just how durable could a hollow ball bearing be? Learners model the strength of the walls of a ball bearing as a function of the radius of its cavity. They use their models to make reasonable conclusions about the probability of failure...
EngageNY
Mathematical Area Problems
Teach the connection between area models and the distributive property through problem-solving. The 22nd activity in a series of 29 explains the distributive property graphically. Learners build area models from word problems and convert...
Mathematics Assessment Project
“Ponzi” Pyramid Schemes
Use mathematics to show your classes the power of a good model. Young mathematicians analyze the famous Ponzi pyramid scheme using an exponential pattern. They make conclusions on the reliability of the plan and why it is illegal.
Channel Islands Film
Natural Resources, and Human Uses of Plants and Animals
As part of their study of the restoration projects on Santa Cruz Island, class members demonstrate their understanding of the connections among plant life, animals, and the actions of humans by crafting a model that reveals these...
CK-12 Foundation
Area and Volume of Similar Solids: Similar Solids
Five questions make up an interactive designed to boosts knowledge of area and volume of solid figures. Question types include multiple-choice, true or false, and fill-in-the-blank. A scale model changes measurement to provide a visual...
Learning for Justice
Change Agents in Our Own Lives
Everyone has the power to change their own lives. Young historians learn how they can become agents for change in their own lives and the community. The lesson focuses on positive role models and what motivates individuals to promote...
EngageNY
Graphs of Quadratic Functions
How high is too high for a belly flop? Learners analyze data to model the world record belly flop using a quadratic equation. They create a graph and analyze the key features and apply them to the context of the video.
EngageNY
The Multiplication of Polynomials
If you can multiply multi-digit integers, you can multiply polynomials. Learners use an area model to compare multiplying numbers to multiplying polynomials. They progress to using the distributive property.
EngageNY
The Division of Polynomials
Build a true understanding of division of polynomials. Learners use their knowledge of multiplying polynomials to create an algorithm to divide polynomials. The area model of multiplication becomes the reverse tabular method of division.
Balanced Assessment
Monitor Pricing
Out with the old and in with the new. Learners use a set of prices of computer monitors from 1994 to make a prediction. They then use one current price and what they know about the old prices to make a more recent prediction. Their...
EngageNY
Comparing Quadratic, Square Root, and Cube Root Functions Represented in Different Ways
Need a real scenario to compare functions? This lesson has it all! Through application, individuals model using different types of functions. They analyze each in terms of the context using the key features of the graphs.
Balanced Assessment
Bathtub Graph
Represent the relationship between independent and dependent variables through a modeling situation. The activity expects learners to graph the volume of water in a bathtub during a given scenario. The graph should result in two areas of...
Concord Consortium
Sticking a Balloon to a Wall
This is one sticky situation! Science sleuths uncover the mystery behind a balloon that appears to be stuck to a wall using an interactive. Learners observe a neutrally charged wall before they manipulate the charge on a balloon. Atom...
Colorado State University
How Far Away Is Space?
Outer space may be a lot closer than you think! Science scholars model the layers of the atmosphere using transparencies to gain insight into the scale of space. The resource includes ideas to tailor the activity to the skill level of...
101 Questions
Small Trebuchet
Travel back to medieval time where learning is just a stone's throw away! A video introduction shows a trebuchet (catapult-like machine) as it launches a rock into a lake. Learners use their quadratic modeling skills to predict the...
Bonneville
Design and Engineer Solutions
What's the best way to collect all that trash? A culminating activity has scholars use the knowledge and skills from the unit to design a solution to the plastic trash island problem. They use 3-D pens or a 3-D printer to build models of...
Center for Math and Science Education
Solar System Launch
Trying to understand the vastness of outer space can be quite a challenge for young scientists. Help put things in perspective with this cross-curricular activity as students work in pairs creating scaled models of...
NYSU
Understand a Fraction as a Number on a Number Line
Piece by piece young scholars build a basic understanding of fractions in a Common Core-designed elementary math lesson. Through a series of hands-on activities and journaling exercises, and with the help of multiple...
CK-12 Foundation
Geometric Sequences and Exponential Functions: Bouncing Ball
Explore a geometric sequence model through a simulation. Learners change the starting drop height of a ball and watch how the heights of following bounces change. They consider the ratio of the consecutive bounces as they analyze...
CK-12 Foundation
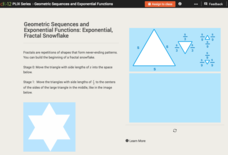
Exponential Growth: Exponential, Fractal Snowflakes
Examine an exponential growth model. Using a fractal, learners calculate the perimeters of each stage. When comparing the consecutive perimeters, a pattern emerges. They use the pattern to build an equation and make conclusions.
Mascil Project
Design a Parking Garage
Parking structures don't build themselves. Investigate the process of designing and planning the construction of a parking garage. After considering the factors that must go into the design, scholars create their own models from a...
Other popular searches
- Clay Modeling
- Modeling Plate Tectonics
- Visual Math Vocabulary
- Computer Modeling
- Modeling Division
- Modeling Quadratic Functions
- Linear Modeling
- Modeling Dna Structure
- Modeling Group Work
- Modeling Day and Night
- Modeling Cell Structures
- Modeling Addition Equations